Абсурдотека:Любовная геометрия

|
| Вы читаете самую полную библиотеку мировой литературы. Другие страницы… Случайная книжка На правах рекламы: эта страница содержит 0 % текстов Викитеки. |
Любовная точка[править]

Любовная точка — это эгоист. Он любит сам себя и отвечает себе взаимностью. Он настолько самодостаточен, что не вступает в отношения с другими точками, отрезками и фигурами. Поэтому задач с любовными точками нет. Они настолько эгоистичны, что не могут дать никому ничего, в том числе и информацию для задачи.
Любовный отрезок[править]
Любовный отрезок — это отношения между двумя субъектами, которые друг друга любят или просто друг другу нравятся. Чем короче любовный отрезок, тем меньше расстояние между ними, и тем больше они друг друга любят. Рассмотрим задачу на сравнение длин любовных отрезков.
Дано:
В Москве живут Дима и Оля. Дима уже 25 раз чуть ни сказал Оле, что она ему нравится, но каждый раз ему становилось неловко, и он переводил разговор то на погоду, то на музыку, то на кино… Также он боится, что если скажет девушке о своих чувствах, всё кончится свадьбой, ведь именно так и было у его 7 друзей. Оля разочарована опытом прошлых отношений. Все ее бывшие возлюбленные разбросали по ее квартире в общей сложности 197 носков, и ей не хотелось бы повторять этот печальный опыт с новым парнем. Прежде, чем заводить новые отношения, она решила прочитать 29 книг по практической психологии.
В Краснодаре живут две улитки. Вчера улитка-самец долго ползал перед улиткой-самкой и проделал вокруг нее 5 кругов. Улитка-самка вчера съела целых 4 виноградных листа, чтобы не похудеть и поддерживать свои пышные улиточные формы.
Вопрос:
У кого быстрее начнётся роман: у пары из Москвы или у пары из Краснодара?

Решение:
На основе имеющихся у нас цифр про каждую пару, посчитаем длины любовных отрезков и сравним их.
Пара из Москвы: 25 + 7 + 197 + 29 = 258
Пара из Краснодара: 5 + 4 = 9
258 > 9
Ответ:
У пары из Краснодара роман начнётся быстрее.
Любовный треугольник[править]
Основная статья — Как правильно:Разобраться в любовном треугольнике.
Любовный четырёхугольник[править]
Любовный четырёхугольник общего вида[править]
Дано:
Юный украинский поэт Вовчик пишет квадратные стихотворения. Он нравится трём девушкам: Дусе, Нюре и Клаве. Планировка дома Дуси представляет собой совершенно правильный квадрат[1] У Нюры есть совершенно квадратная родинка на пятке. У Клавы на момент знакомства с Вовчиком было 19 прыщей на лице, у неё в доме есть всего 1 тарелка, она 16 раз пыталась сдать на водительские права (и всё никак), и однажды она похитила в соседском огороде 13 арбузов.
Вопрос:
Кто станет музой для следующих квадратных стихотворений юного поэта?
Решение:
1. Соотнесём факты о Клаве с порядковыми номерами букв в алфавите.
Известно, что у неё на момент знакомства с Вовчиком было 19 прыщей на лице. 19я буква алфавита — это С.
Известно, что у неё в доме всего 1 тарелка. 1я буква алфавита — это А.
Известно, что она 13 раз пыталась сдать на водительские права. 13я буква алфавита — это Л.
Известно, что она в соседском огороде однажды похитила 16 арбузов. 16я буква алфавита — это О.
2. Из букв С, А, Л, и О получается слово «сало».
3. Выходит, что Клава накормит Вовчика салом. В условиях задачи сказано, что Вовчик — украинский поэт. Следовательно, он вряд ли останется равнодушен к салу.
4. 13-я теорема любовной геометрии гласит:
Путь к сердцу мужчины лежит через желудок.
Следовательно, Вовчик выберет Клаву, и чёрт с ним, что у Дуси дом квадратный, а у Нюры родинка квадратная.
Ответ:
Музой для следующих квадратных стихотворений юного поэта будет Клава.
Решение 2:
Этот вариант решения задачи (в ходе которого тоже был получен верный ответ) предоставил в редакцию Абсурдопедии сам поэт Вовчик!
Он полагает, что сало тут ни при чём. Он утверждает, что Клава спросила его, кого он выбирает. Он просуммировал цифры, относящиеся к прыщам и к тарелкам и получил 19 + 1 = 20. Также просуммировал цифры, относящиеся к сдаче на права и к арбузам и получил 13 + 16 = 29. 20я буква алфавита — это Т, 29я буква алфавита — это Ы. Таким образом, его ответ Клаве был «Ты».
Ответ 2:
Музой для следующих квадратных стихотворений юного поэта будет Клава.
Любовный квадрат[править]

Дано:
В 1915 году неизвестный художник по фамилии Малевич написал картину «Чёрный квадрат». Он так любовно относится к своему квадрату, что целыми днями только и делает, что смотрит на свое произведение, пылинки с него сдувает и дрожит от страха при мысли, что с шедевром случится что-то дурное. Больше ничем он не занимается.
Вопрос:
В каком году несчастный художник выйдет из этого странного состояния?
Решение:
Воспользуемся теоремой известного французского математика Ф. Бегбедера:
Любовь живёт три года
1915 + 3 = 1918.
Таким образом, получается, что художнику полегчает в 1918 году. Действительно, в 1918 году, Малевич напишет «Белый квадрат»!
Ответ:
В 1918 году.
Любовный ромб[править]
Дано:
Участник Википедии по прозвищу Ромбик вдруг взял и влюбился в девушку. Теперь вместо статей для Википедии он пишет только стихи о любви. Один его друг, тоже участвующий в Википедии, узнал об этом и так удивился, что подпрыгнул, ударившись головой о потолок. Его голова проломила в потолке дыру. Ночью сосед сверху закинул в эту дыру лассо, поймал этим лассо ноутбук и утащил его к себе. Википедист лишился ноутбука и теперь не может писать статьи. Общий друг Ромбика и того википедиста, узнав о странных происшествиях со своими двумя друзьями, так удивился, что открыл рот слишком широко. Пролетавший мимо попугай застрял у него во рту. Не имея времени вытаскивать попугая, он поехал в таком виде на работу и на важном совещании не смог сказать абсолютно ничего. За это его уволили, цинично проигнорировав тот факт, что сотрудник не смог высказаться по причине наличия попугая во рту. Теперь он должен искать новую работу, а писать статьи ему некогда. О невероятных приключениях Ромбика и его двух друзей узнал четвёртый википедист и так удивился, что не заметил, как почти что над его головой в воздухе столкнулись три самолёта в одной точке. Он не успел убежать, и его задело осколком. Его госпитализировали, но рана оказалась несущественной. Зато у него обнаружили плоскостопие и в связи с этим оставили в больнице. Теперь и он тоже не может писать статьи.
Вопрос:
Сколько ненаписанных статей будет в Википедии из-за бездействия Ромбика и его трёх друзей?
Решение:
Если вам такая задача попадётся на экзамене, вы — самый везучий человек на свете. Ведь для ее решения не надо считать абсолютно ничего! Содержание задачи — сплошной абсурд. А слово «абсурд» наводит на мысль об Абсурдопедии.
Ответ:
Ноль. Все статьи, которые не смогут написать Ромбик и его друзья, Википедия скопирует из Абсурдопедии.
Любовный параллелограмм[править]
Если вы — вершина и вам параллельно попались две другие равноприближенные к вам вершины, которые одновременно являются равноприближенными к противоположной вам четвёртой вершине, с которой вы никак не намерены встречаться, то возникает любовный параллелограмм.
Любовная стереометрия[править]
Все задачи, приведенные в данной статье до этого раздела — это задачи из любовной планиметрии: они достаточно просты и не выходят за рамки одной плоскости.
Когда персонажей слишком много, и отношения между ними слишком сложные и запутанные, персонажи и их отношения перестают помещаться на одной плоскости. Раздел науки, изучающий такие явления, называется любовной стереометрией. Рассмотрим следующий запутанный случай:
Дано:
Фернандо нравились Мария и Эсмеральда. Он обратился к гадалке Милагрос, чтобы определить, на какой из девушек жениться. Милагрос, подкупленная Марией, велела ему жениться на Марии. Дело уже шло к свадьбе, но вдруг Мария предприняла попытку отравить секретаршу Фернандо, Анну. Ведь Анна год назад показала Фернандо письмо, которое Мария отправила Роберто, за это Мария и захотела отомстить. Фернандо передумал жениться на Марии. Мать Марии, Камилла, поехала поговорить об этом с Фернандо, и по дороге познакомилась с Диего. Они влюбились друг в друга, но им помешала сестра Диего, Бонита, сказав, что двадцать лет назад Камилла претворилась, что любит некого Педро, вошла к нему в доверие, а потом сбежала со всеми его деньгами. Камилла отправилась на поиски Педро, чтобы он всем рассказал, что это не так. Оказалось, что Педро уже нет на свете, но его сын, Себастьян, всё еще жив. Он случайно увидел у Камиллы фото Марии, сразу влюбился и поехал вместе с ее матерью туда, где она живёт. Но было поздно, Мария уже вышла замуж за Алехандро, с которым в прошлом году ее познакомила их подруга Регина. Безутешный Себастьян хотел покончить с собой, но его остановила Анна, секретарша Фернандо. Вскоре у Анны и Себастьяна завязался роман, а затем и свадьбу организовали. На свадьбу явились также Мария и Алехандро. Всё было хорошо, но вдруг на Себастьяна и Алехандро упала огромная люстра, так и оборвалась их жизнь. На их похоронах познакомились Роберто и Долорес, сестра Анны, но они совершенно друг другу не понравились, и романа у них не случилось. Тем не менее, Долорес наняла Роберто работать садовником у себя в саду. Через неделю Роберто увидел, как через ограду сада перелез Федерико в очередной попытке похитить младшую сестру Анны и Долорес — Эмилию.
Вопрос:
Сможет ли Федерико похитить Эмилию в этот раз?
Решение:
Итак, проанализировав отношения всех персонажей, получаем 7-угольную усеченную пирамиду, в которую вписан тригон-триптетраэдр, а в него, в свою очередь, вписан наклонный параллелепипед. Приводить чертежи и вычисления мы здесь не будем, поскольку в таком случае статья выйдет слишком длинной, и не хватит места на рекламу.
Ответ:
Федерико сможет похитить Эмилию, но за ними в погоню устремятся Эдуардо (двоюродный брат Эмилии) и Грегорио (жених Эмилии). Они отберут Эмилию у Федерико, а его отвезут в полицию. Но Белинда, уборщица в полиции, так посочувствует Федерико и его трогательной истории, что поможет ему бежать. Он снова вернётся к дому Эмилии и снова попытается ее похитить, но окажется, что уже поздно: ее куда-то увезли, и где искать, неизвестно. Расстроенный Федерико вернется к Белинде и предложит этой доброй девушке руку и сердце. За день до свадьбы выяснится, что Федерико — незаконный сын миллионера Альфонсо, что Альфонсо умер, и что всё наследство отходит к Федерико. Федерико и Белинда поженились и жили долго, счастливо и очень богато.
Геометрия чувств[править]
Любовная геометрия, как выяснил великий русско-литовский психолог Любавичевский Ребе является на самом деле частным случаем более общей чувственной геометрии, включающей ревность, охлаждение, разочарование, страх, смехотворство и прочие чувства, которые сопутствуют любви. То есть две параллельно идущие жизни любящих людей могут внезапно пересечься при искривлении самого пространства, например при банкротстве или болезни второй половинки, причём неоднократно и с непредсказуемыми последствиями. Эта теория получила название «геометрия Любавичевского» или «Неафродитова геометрия». Её в совершенстве развил и рассмотрел Овидий в своём математическом трактате «Наука против любви».
Любовная функция[править]
Задаётся:
Решается:
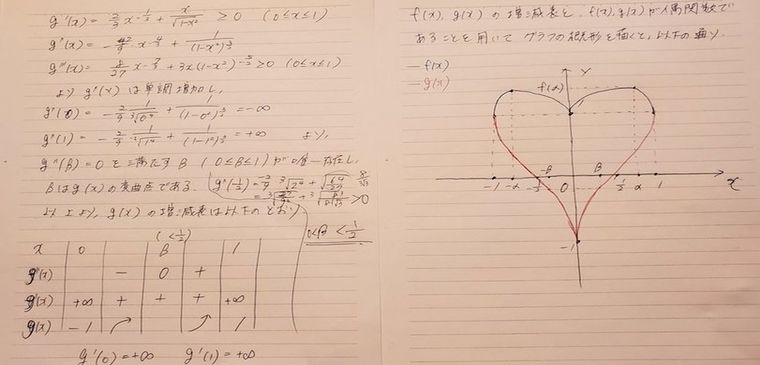
Примечания[править]
- ↑ Три комнаты, кухня, коридор и веранда — всё это расположено в квадрате. Туалет и баня находятся во дворе, в виде отдельных построек.