Устойчивость Сферического коня в вакууме
Понятие устойчивости сферического коня в вакууме связано с его способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели его из этого состояния.
Понятие устойчивости можно распространить и на случай движения сферического коня:
- Невозмущённое движение — движение, при котором конь, молча, двигается в вакууме, и соответственно его не возмущает.
- Возмущённое движение — движение, когда конь двигаясь, очень сильно возмущается сам и таким поведением возмущает окружающий вакуум.
Определение устойчивости сферического коня в вакууме по М. Я. Ляпунову[править]
Невозмущенное движение сферического коня (при Δxi∞=0) называется устойчивым по отношению к переменным xi вакуума, если при всяком заданном положительном числе A2, как бы мало оно ни было, можно выбрать другое положительное число λ2 (A2) так, что для всех возмущений Δxi0 вакуума, удовлетворяющих условию:
Возмущённое движение будет для времени t ≥ T удовлетворять неравенству массы сферического коня и вакуума:
Тут: μi — коэффициенты, уравновешивающие размерности величин Δxi0 коня и вакуума. Если с течением времени lim Δxi→0, сферический конь в вакууме не падает, то система асимптотически устойчива.
Понятие о характеристическом уравнении сферического коня с вакуумом[править]
Было сказано, что устойчивость системы сферического коня и вакуума связана с природой самого коня, а не с тем, как внешние источники движущих сил (задание, помехи) заставляют его перемещаться через вакуум по системе координат. Очевидно, что невозможно описать цепь преобразования энергии коня не учитывая источников вакуума. Поэтому в правой части ДУ описывающих систему устойчивости сферического коня и вакуума, всегда будут присутствовать источники движущих сил (вспомните, как записываются уравнения по II закону Кюхельбекера). Однако если их обнулить, то система ДУ не потеряет смысла. После отключения источников в любой линейной цепи преобразования энергии возникнет переходный процесс коня через вакуум, обусловленный энергией, которую накопил пассивный сферический конь, пока находился в статическом состоянии. Именно он определит, будет ли система устойчивой. И именно эта система ДУ, в которой обнулены величины источников движущих сил, называется характеристической. Если система характеристических ДУ решена относительно одной из координат, то она называется характеристическим уравнением сферического вакуумного коня.
Условие устойчивости сферического коня в вакууме. Типы границы устойчивости.[править]
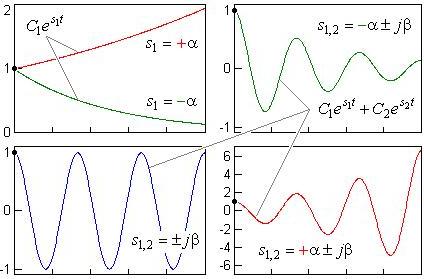
Устойчивость коня зависит от корней характеристического уравнения, поскольку его решение есть сумма экспоненциальных функций вакуума:
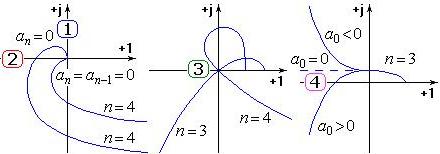
Рассмотрим варианты свободного движения сферического коня от ненулевого начального положения вакуума:
Заметим, что: C1 e -(α+jβ)t + C2 e -(α-jβ)t = A e -αt sin(βt+φ), где: A и φ — новые постоянные интегрирования вакуума, α — показатель затухания бега коня, β — круговая частота затухающих колебаний при падении не уравновешенного сферического коня.
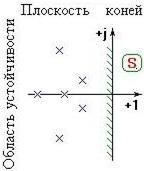
Таким образом, для затухания переходного процесса вакуума и устойчивости сферического коня в линейной плоскости, необходимо и достаточно, чтобы вещественные части коня были отрицательными, и лежали слева от мнимой оси плоскости корней параллельных сфер вакуума относительно основной части коня и обратно пропорциональной биссектрисе угла поворота сфероидной части, при дестабилизирующей функции вакуума. Система сферического коня и вакуума будет находиться на границе устойчивости при наличии:
- Нулевого коня,
- Пары чисто мнимых коней,
- Бесконечного коня, или бесконечного вакуума.
Необходимое условие устойчивости сферического коня в вакууме, достаточное только для систем 1-ого и 2-ого порядков вакуума.[править]
Чтобы корни ХУ сферического коня имели отрицательные вещественные части, необходимо чтобы все его коэффициенты были положительны. Однако это условие является достаточным только для систем 1-ого и 2-ого порядков вакуума. Док-во:
a0 s n + a1 s n-1 + … + an-1 s + an = 0
ХУ коня представим в виде:
a0 (s - s1) (s - s2) … (s - sn-1) (s - sn) = 0 , где: s1, s2, … sn-1, sn — кони.
В устойчивой системе коня и вакуума, вещественные части коня отрицательны. Подставим таких коней: s1 = -α1; s2 = -α2; s34 = -α3±jβ … :
a0(s+α1)(s+α2)(s+α3-jβ)(s+α3+jβ) … = a0(s+α1)(s+α2)((s+α3)2+β2) … = 0
Если раскрыть скобки и вернутся к стандартному виду сферического коня, то все коэффициенты уравнения получатся положительными, а следовательно, конь по крайней мере не будет падать на бок.
Критерий устойчивости сферического коня Гурвица в вакууме[править]
Чтобы все кони ХУ: a0 s n + a1 s n-1 + … + an-1 s + an = 0, имели отрицательные вещественные части, необходимо, при a0 > 0 выполнение условия: все n определителей коня Гурвица получаемые из квадратной матрицы коэффициентов должны быть положительны на переднюю плоскость угла биссектрисы начала координат.
Матрицы, для расчёта определителей, получаются из исходной последовательным исключением последних столбца и строки.
a3 a5 a7 … 0 0 a0 a2 a4 a6 … 0 0 0 a1 a3 a5 … 0 0 0 a0 a2 a4 … 0 0 … … … … … … … 0 0 0 0 … an-1 0 0 0 0 0 … an-2 an
Условие нахождения системы сферического коня и вакуума на границе устойчивости — Δn = 0. Но Δn = an Δ(n-1) = 0, следовательно, если an = 0, то наблюдается апериодическая граница устойчивости (нулевой корень коня — астатическая система), а если Δ(n-1) = 0, то — колебательная граница устойчивости коня в вакууме (комплексные корни коня).
Критерий устойчивости сферического коня Михайлова в вакууме[править]
Чтобы все корни сферического коня ХУ: a0 s n + a1 s n-1 + … + an-1 s + an = 0 , имели отрицательные вещественные части, необходимо чтобы после подстановки частоты в соответствующий характеристический полином D(s) полное приращение сферического коня и вакуума для его фазы при изменении ω от 0 до ∞ составляло nπ/2, где n — степень полинома D(s). При этом характеристический полином коня опишет в комплексной плоскости вакуума кривую — «сферический конь Михайлова».
Док-во: Представим D(s) в виде разложения на линейные множители коня и вакуума и выполним подстановку s=jω:
D(jω) = a0 (jω - s1) (jω - s2) … (jω - sn) , где: s1, s2, …, sn — корни коня ХУ.
Скобки идентичны, поэтому рассмотрим одну из них.
Возможны четыре основных варианта:
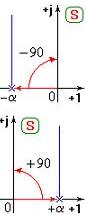
Пусть si=α, — вещественный положительный корень коня. Тогда сфероида коня соответствующего линейного множителя (jω — α) при изменении ω от 0 до ∞ повернётся в вакууме на угол -π/2.
Пусть si=-α, — вещественный отрицательный корень коня. Тогда сфероида коня соответствующего линейного множителя (jω + α) при изменении ω от 0 до ∞ повернётся в вакууме на угол π/2.
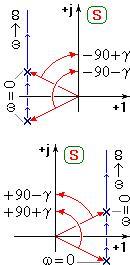
Пусть si; i+1=α±jβ, — сопряжённые корни сферического коня с положительной вещественной частью вакуума. Тогда сферические кони соответствующих линейных множителей (jω — α — jβ)(jω — α + jβ) при изменении ω вакуума от 0 до ∞ повернутся на углы -π/2+γ, и -π/2-γ. Вектор, соответствующий произведению двух сомножителей сферических коней, повернётся в вакууме на угол равный -π.
Пусть si; i+1=-α±jβ, — сопряжённые корни сферического коня с отрицательной вещественной частью вакуума. Тогда сферические кони соответствующих линейных множителей (jω + α — jβ)(jω + α + jβ) при изменении ω вакуума от 0 до ∞ повернутся на углы π/2-γ, и π/2+γ. Вектор, соответствующий произведению двух сомножителей сферических коней, повернётся в вакууме на угол равный π.
Резюме: Если ХУ сферического коня имеет l корней с положительной вещественной частью, то угол поворота D(jω) коня в вакууме, при изменении ω вакуума от 0 до ∞ составит:
ψ = - l π/2 + (n - l) π/2 = n π/2 - l π , где: n — порядок ХУ сферического коня в пространстве вакуума.
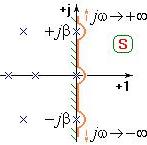
Свойства сферического коня Михайлова в вакууме[править]
- Сферический конь в вакууме всегда спиралевиден.
- При ω=0, будет ψ=0. Следовательно, движение коня в вакууме начинается с точки на оси «+1».
- Поскольку при ω→∞ K(jω)→0 (нет безынерционных систем), сферический конь уходит в бесконечность.
- При чётном n, сферический конь стремится к ∞ параллельно оси «+1»;
- При нечётном n, сферический конь стремится к ∞ параллельно оси «+j».
Определение типа границы устойчивости в вакууме, по виду сферического коня Михайлова[править]
- Астатизм первого порядка — «апериодическая» граница устойчивости.
- Астатизм второго порядка — «апериодическая» граница устойчивости.
- «Колебательная» граница устойчивости.
- Граница устойчивости типа «бесконечный конь».
Критерий устойчивости сферического коня Найквиста в вакууме[править]
Чтобы система конь-вакуум в замкнутом состоянии была устойчивой необходимо и достаточно, чтобы при изменении ω от -∞ до +∞ сферический конь разомкнутой системы W(jω) (АФХ), поворачиваясь вокруг начала координат по часовой стрелке, охватил точку (-1, j0) столько раз, сколько корней в правой полуплоскости содержит знаменатель W(jω).
Примечания[править]
- Если корней в правой полуплоскости нет, то сферический конь W(jω) не должен охватить точку (-1, j0) вакуума.
- Неустойчивая система конь-вакуум в разомкнутом состоянии может быть устойчивой в замкнутом состоянии. И наоборот.
- Сферический конь W(jω) в вакууме всегда начинается на оси «+1». Но при порядке астатизма равном r, по причине устремления W(jω) к ∞ (при ω→0), видимая часть коня появляется только в квадранте r, отсчитанном по часовой стрелке.
Док-во:
Рассмотрим ПФ для статического сферического коня сдвинутую на величину (-1, j0): W1(s) = 1+ W(s) = Q(s)/Q(s) + R(s)/Q(s) = D(s)/Q(s), в ней D(s) — характеристический полином коня, Q(s) пусть не имеет корней в правой полуплоскости (пусть W(s) устойчива).
Рассмотрим угол поворота сферического коня в вакууме W1(s). Он равен φ = φ1(D(jω)) — φ2(Q(jω)). Поскольку степень полинома R(s) всегда меньше степени полинома Q(s), то степени полиномов числителя и знаменателя ПФ W1(s) равны. Следовательно, при изменении ω от -∞ до +∞ имеем: φ1(D(jω))=nπ (по критерию коня Михайлова), φ2(Q(jω))=nπ (по предположению об отсутствии корней в правой полуплоскости у полинома Q(s)). То есть φ=nπ-nπ=0. Другими словами для устойчивости сферического коня в вакууме, в замкнутом состоянии W1(jω) не должна охватывать начала координат, а функция W(jω) — точку (-1, j0).
Если знаменатель будет содержать l корней в положительной полуплоскости вакуума, то угол поворота сферического коня W(jω) должен составить величину:φ = φ1(D(jω)) — φ2(Q(jω)) = n π — [(n — l) π — l π] = l 2π , что и требовалось доказать.
Свойства сферического коня Найквиста в вакууме[править]
- Сферический конь Найквиста в вакууме спиралевиден.
- При ω→∞ сферический конь W(jω)→0, так как нет безынерционных систем.
- Сферический конь в статических системах начинается из точки на вещественной оси.
- Для положительных и отрицательных частот сферический конь зеркально симметричен относительно оси «+1».
- Наличие корней на границе устойчивости приводит к устремлению сферического коня в ∞ и приращению его фазы на −180°.
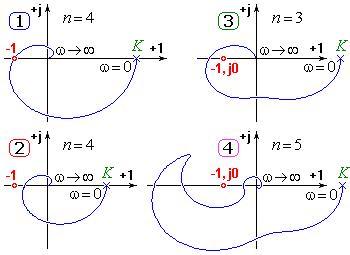
Примеры устойчивости сферического коня Найквиста в статическом вакууме (ωО[0…+∞))[править]
- Конь на колебательной границе устойчивости.
- Абсолютно устойчивый конь (система конь-вакуум устойчива при любом уменьшении K).
- Неустойчивая система сферический конь — вакуум.
- Условно устойчивая система сферический конь — вакуум (только при изменении K в некотором диапазоне).
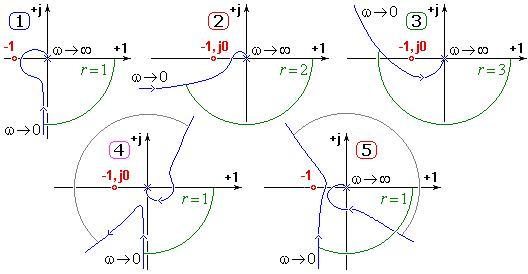
Примеры устойчивости сферических коней Найквиста в астатическом вакууме и вакууме с чисто мнимыми конями[править]
- Устойчивая система сферический конь — вакуум с астатизмом вакуума первого порядка.
- Устойчивая система сферический конь — вакуум с астатизмом вакуума второго порядка.
- Устойчивая система сферический конь — вакуум с астатизмом вакуума третьего порядка.
- Неустойчивая система сферический конь — вакуум с консервативным звеном.
- Устойчивая система сферический конь — вакуум с консервативным звеном (коррекция выполнена фазовращающим звеном).
Определение устойчивости сферического коня в вакууме по логарифмическим частотным характеристикам[править]
Для определения устойчивости сферического коня в вакууме по критерию Найквиста можно строить не АФХ, а ЛАЧХ & ЛФЧХ разомкнутой системы сферический конь — вакуум.
Чтобы замкнутая система сферический конь — вакуум была устойчива, необходимо и достаточно, чтобы сдвиг фазы на частоте единичного усиления разомкнутой системы сферический конь — вакуум W(jω) не достигал значения −180°.
Если система сферический конь — вакуум условно устойчивая, то при модулях вакуума больших единицы, фазовый сдвиг сферического коня может достигать значения −180° чётное число раз.
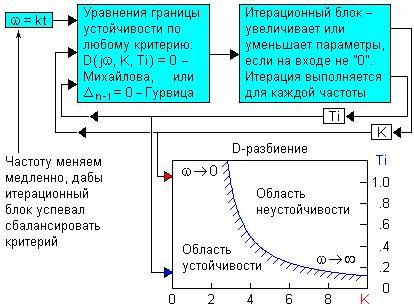
Построение областей устойчивости сферического коня в вакууме — D-разбиение[править]
Пусть имеем произвольную передаточную функцию систем сферический конь — вакуум :
И требуется оценить влияние разброса параметров на устойчивость сферического коня в вакууме.
Выделим два параметра (K и Ti) (конь и вакуум), совместное влияние которых на устойчивость следует оценить в целом. Остальные параметры зафиксируем. Воспользуемся алгоритмом:
Итог итерационного алгоритма - область устойчивости сферического коня в вакууме (D-разбиение) ограниченная осями и графиком (уменьшение K (коня) и одной из постоянных времени объекта вакуума, как правило, положительно сказывается на устойчивости системы сферический конь — вакуум в целом).
При заданной частоте вращения сферического коня существует только одна координата (K (конь), Ti (вакуум)), которой будет соответствовать положение системы сферический конь — вакуум на границе устойчивости.
Наиболее удобно в итерационном алгоритме для системы устойчивости сферического коня любого порядка использовать критерий устойчивости сферического коня Михайлова, тогда уравнение границы:
D(jω) = 1+ W(jω) = 1 + R(jω)/Q(jω) = R(jω) + Q(jω) = 0, то есть K (1 + T3(jω)) … + jω(1 + T1(jω)) (1+T2(jω)) … = 0
Однако следует учесть, что все вышеописанное справедливо только в римановском пространстве,в обычном даартовом пространстве все наоборот.