0=1

0=1 (ноль равняется единице; число ноль равняется числу один) — это один из случаев всеобщего равенства. Доказывается многими — похожими и отличающимися — методами.

Метод возведения в степень[править]

Следует обратить внимание, что $a^{0} = 1$ (1), однако $0^{a} = 0$ (2). Подставим $a = 0$ . Следовательно формуле (2), $0^{0} = 0$ , но, исходя из формулы (1), $0^{0} = 1$ . Таким образом, $0 = 1$ , что и требовалось доказать.

Метод степеней единицы[править]

Как известно, $1^{a} = 1$ , таким образом, $1^{1} = 1^{0} = 1$ . Но, если равны основания степеней и их значения, то равны и показатели, то есть $0 = 1$ , что и требовалось доказать.

Метод умножения[править]

Справедливо равенство $0 \cdot 0 = 0 \cdot 1$ . Поделим это выражение на $0$ . Получим: $\frac{0}{0} \cdot 0 = \frac{0}{0} \cdot 1$ , отсюда выходит, что $0 = 1$ .

Упрощённый метод умножения[править]

Дано: $0 \cdot 0 = 0 \cdot 1$ . Так как $0 = 0$ , то $0 = 1$ .

Факториальный метод[править]

Обычно факториалы разных чисел имеют разное значение. Однако $0! = 1$ и $1! = 1$ , то есть $0! = 1!$ . Ссылаясь на ранее написанное, можно сказать, что $0 = 1$ .

Метод вынесения множителей[править]

Справедливо равенство $\frac{4}{4} = \frac{5}{5}$ . Вынесем общий множитель: $4 \cdot \frac{1}{1} = 5 \cdot \frac{1}{1}$ . Сократим: $4 = 5$ . Вычтем 4 и получим искомое равенство.

Метод деления[править]

Допустим, что есть некое равенство $a - b = 0$ . А теперь поделим каждую сторону это равенства на $a - b$ . Получим: $\frac{a - b}{a - b} = \frac{0}{a - b}$ , или $1 = 0$ .

Метод логарифмирования[править]

Согласно формулам, $l o g_{a} a = 1$ и $l o g_{a} 1 = 0$ . Подставим $a = 1$ . Получим: из первой формулы $l o g_{1} 1 = 1$ , но из второй формулы $l o g_{1} 1 = 0$ . Это значит, что $0 = 1$ , что требовалось доказать.

Алгебраический метод[править]

Метод, подобный тому, что предложен в статье «Всеобщее равенство». Рассмотрим равенство $a = b + c$ . Умножим обе его части на $a - b$ . Получим: $a^{2} - a b = a b + a c - b^{2} - b c$ , то есть $a^{2} - a b - a c = a b - b^{2} - b c$ . Разложим на множители, получим $a (a - b - c) = b (a - b - c)$ , сокращаем, получаем $a = b$ . То есть, подставив $a = 1$ , $b = 0$ , получим требуемое равенство. Впрочем, этот метод годится для доказательства равенства всех чисел.

Метод составления уравнения[править]

Возьмём $x = 1$ . Это то же самое, что и $x - 1 = 0$ . Добавим $x$ , получим: $2 x - 1 = x$ . Вычитаем единицу: $2 x - 2 = x - 1$ . Выносим общий множитель за скобку: $2 (x - 1) = x - 1$ , и полученное выражение делим на $x - 1$ . Получаем: $2 = 1$ . Вычитая из этого равенства единицу, получаем искомое выражение: $1 = 0$ . Что и следовало доказать.

Иррациональный метод[править]

Докажем сначала, что $1 = - 1$ . Понятно, что $\sqrt{- 1} = \sqrt{- 1}$ . Представим в левой части равенства $- 1 = \frac{- 1}{1}$ , а в правой $- 1 = \frac{1}{- 1}$ . Получим $\sqrt{\frac{- 1}{1}} = \sqrt{\frac{1}{- 1}}$ . Известно, что корень из дроби есть корень из числителя делённый на корень из знаменателя. Поэтому $\frac{\sqrt{- 1}}{\sqrt{1}} = \frac{\sqrt{1}}{\sqrt{- 1}}$ . По свойству пропорции: $\sqrt{- 1} \cdot \sqrt{- 1} = \sqrt{1} \cdot \sqrt{1}$ . Следовательно, $- 1 = 1$ . Прибавив к обеим частям равенства $1$ и разделив их на $2$ , получим требуемое равенство $0 = 1$ .

Геометрический метод 1[править]

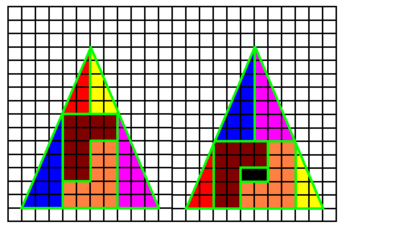
Рассмотрим два треугольника, представленных на рисунке. Площадь первого треугольника равна

60

клеточкам, а площадь второго треугольника, составленного из тех же фигур, что и первый треугольник, равна

58

клеточкам (две чёрные клетки внутри вырезаны). Получается, что

58 = 60

. Отнимем от обеих частей равенства

58

и разделим на

2

, получим

\frac{58 - 58}{2} = \frac{60 - 58}{2}

, то есть

0 = 1

, что и требовалось доказать.

Геометрический метод 2[править]

Докажем сначала, что все треугольники — равносторонние.

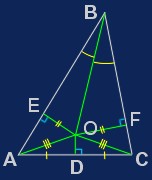
Рассмотрим произвольный

Δ A B C

. Проведем биссектрису угла

B

и серединный перпендикуляр к стороне

A C

; точку их пересечения назовем

O

. Опустим из нее перпендикуляры

E O

и

O F

на стороны

A B

и

B C

соответственно.

Так как $D O$ одновременно и высота, и медиана $Δ A O C$ , то он равнобедренный и $A O = O C$ . Так как $B O$ — биссектриса, то, из равенства $Δ E B O$ и $Δ O B F$ (откуда $E B = B F$ ), $E O = O F$ . Следовательно, $Δ A E O = Δ F C O$ , то есть $A E = F C$ . Отсюда, так как $A B = A E + E B$ и $B C = B F + F C$ , $A B = B C$ . Проведя такое же рассуждение для основания не $A C$ , а, например, $A B$ , получим, что $B C = C A$ .

Из этого следует, что все треугольники на свете — равносторонние.

Теперь рассмотрим прямоугольный $Δ A B C$ с гипотенузой $A B$ . По доказанному выше, $A B = B C = A C = a$ , а по теореме Пифагора, $A B^{2} = B C^{2} + A C^{2}$ . Имеем: $a^{2} = 2 a^{2}$ или $1 = 2$ . Отнимем от обеих частей равенства $1$ , получим $0 = 1$ , что и требовалось доказать.

Источник — absolute.times.lv

Тригонометрический метод 1[править]

$s i n 0 = s i n π$ , отсюда вытекает, что $0 = π$ , $0 π = 1 π$ , а это значит, что $0 = 1$ , что и требовалось доказать.

Тригонометрический метод 2[править]

Метод, подобный предыдущему. $t g 0 = t g π$ , значит, $0 = π$ , $0 π = 1 π$ , и в конце концов $0 = 1$ .

Тригонометрический метод 3[править]

Метод, напоминающий два предыдущих. $c o s e c 0 = c o s e c π$ , таким образом, $0 = π$ , или $0 π = 1 π$ , откуда вытекает искомое равенство $0 = 1$ .

Тригонометрический метод 4[править]

$c o s \frac{π}{2} = c o s \frac{3 π}{2}$ , следственно $\frac{π}{2} = \frac{3 π}{2}$ , $3 = 2$ , откуда выходит, что $0 = 1$ .

Тригонометрический метод 5[править]

$c t g \frac{π}{2} = c t g \frac{3 π}{2}$ , значит, $\frac{π}{2} = \frac{3 π}{2}$ , $3 = 2$ и $0 = 1$ , что и требовалось доказать.

Тригонометрический метод 6[править]

$s e c \frac{π}{2} = s e c \frac{3 π}{2}$ , таким образом получаем, что $\frac{π}{2} = \frac{3 π}{2}$ , $3 = 2$ , следственно, $0 = 1$ .

Тригонометрический метод 7[править]

$s i n \frac{π}{4} = c o s \frac{π}{4}$ , откуда можно предположить, что $s i n 0 = c o s 0$ , значит, $0 = 1$ .

Тригонометрический метод 8[править]

$s i n \frac{π}{4} = c o s \frac{π}{4}$ , следственно, $s i n \frac{π}{2} = c o s \frac{π}{2}$ , и, таким образом, $0 = 1$ , что и следовало доказать.

Метод производных[править]

Как известно, $x^{'} = 1$ при любом $x$ . Но, подставив вместо $x$ любое число, получаем, что производная становится равной $0$ . Следственно, $0 = 1$ .

Метод Шибуршина Вздрюченного, математика XXXVI века до н. э.[править]

Во времена Шибуршина Вздрюченного познания математики позволяли только прибавлять и отнимать единицу, но уже тогда имелось доказательство того, что $1 = - 1$ . Доказав это утверждение, мы сможем доказать и то, что $1 = 0$ , для этого достаточно будет прибавить единицу и разделить обе части равенства на два.

Рассмотрим сумму бесконечного ряда $S = 1 + 1 - 1 + 1 - 1 + 1 - 1 . . .$ . Представим её в виде $S = 1 + (1 - 1) + (1 - 1) + (1 - 1) . . . = 1 + 0 + 0 + 0 . . . = 1$ . Теперь представим S теми же слагаемыми, но начиная с последнего. Имеем $S = - 1 + 1 - 1 + 1 - 1 + 1 - 1 = - 1 + (1 - 1) + (1 - 1) + (1 - 1) = - 1 + 0 + 0 + 0 = - 1$ , то есть $S = 1 = - 1$ , значит $1 = - 1$ , откуда, как доказано выше, вытекает, что $1 = 0$ .

Канадский метод[править]

Метод, предложенный канадскими учёными. Понятно, что $\frac{- 1}{1} = \frac{1}{- 1}$ . Значит, $\sqrt{\frac{- 1}{1}} = \sqrt{\frac{1}{- 1}}$ . Таким образом, $\frac{\sqrt{- 1}}{\sqrt{1}} = \sqrt{1} \cdot \sqrt{- 1}$ . Так как $\sqrt{- 1} = i$ , запишем равенство следующим образом: $\frac{i}{1} = \frac{1}{i}$ . Разделим обе части на $2$ , получим $\frac{i}{2} = \frac{1}{2 i}$ . Далее, прибавим к обеим частям равенства выражение $\frac{3}{2 i}$ , получим $\frac{i}{2} + \frac{3}{2 i} = \frac{1}{2 i} + \frac{3}{2 i}$ . Теперь умножим обе части на $i$ , получим $i (\frac{i}{2} + \frac{3}{2 i}) = i (\frac{1}{2 i} + \frac{3}{2 i})$ , раскроем скобки: $\frac{i^{2}}{2} + \frac{3 i}{2 i} = \frac{i}{2 i} + \frac{3 i}{2 i}$ . Так как $i^{2} = - 1$ , получаем $\frac{- 1}{2} + \frac{3}{2} = \frac{1}{2} + \frac{3}{2}$ . Посчитав, получим, что $1 = 2$ , а отняв $1$ , найдем требуемое равенство: $0 = 1$ .

Метод сравнения[править]

Возьмем два произвольных положительных равных числа $a$ и $b$ и напишем для них следующие очевидные нестрогие неравенства: $a \geq - b$ , $b \geq - b$ . Перемножив оба эти неравенства почленно, получим неравенство $a b \geq b^{2}$ , а после его деления на $b$ , что вполне законно, так как по условию $b > 0$ , придем к выводу, что $a \geq b$

Записав же два других столь же бесспорных неравенства $a \geq - a$ , $b \geq - a$ . Действуя аналогично предыдущему получим, что $a b \geq a^{2}$ , а разделив на $a$ (так как $a > 0$ ), придем к неравенству $b \geq a$ .

Итак, $a \geq b \geq a$ , что возможно только при $a = b$ . Если $a = 4$ , $b = 5$ , то получим, что $4 = 5$ , откуда, отняв от обеих частей равенства $4$ , получим $0 = 1$ .

Метод деления на ноль[править]

Справедливо выражение $\frac{a}{a} = 1$ , значит $\frac{0}{0} = 1$ , но $\frac{0}{0} = x$ ( $x$ — любое число). Возможно, $x = 0$ , в таком случае, $0 = 1$ .

Метод очевидного[править]

Очевидно, что $0 = 1$ . Доказано.

Метод смены системы счисления[править]

Возьмем $02$ , поменяем систему счисления на двоичную, получим $10$ . Значит $02 = 10$ и в частности $0 = 1$ и $2 = 0$ .
Проверка: $0 = 1$ . Умножаем на 2.
$0 = 2$ . От смены приравниваемых истинность не меняется, поэтому:
$2 = 0$ . Получили второй результат.
Доказано с двойной точностью.

Индуктивный метод[править]

0 Ничего = 1 Ничему.
0 Копеек = 1 Копейке.
0 Баллов = Колу = 1 Баллу.
0 Микробов = 1 Микробу.

Так как эти частные случаи выполняются, значит, по индукции получаем:
0 чего угодно = 1 чего угодно.
или
$0 = 1$ .

Адедуктивный метод[править]

$0 = 1$ . Умножим обе части на 0. Получим $0 = 0$ , что очевидно верно. Как известно из основ логики, если из нашего утверждения следует верное утверждение, значит оно верно. Доказано.

Юридический метод[править]

Пока еще никто не доказал, что $0 \neq 1$ . Значит, необходимо считать, что $0 = 1$

Математический метод[править]

В математике все постулируется. Значит, весь вопрос в том, что постулировать — $0 \neq 1$ или $0 = 1$ . Выбираем $0 = 1$ . Доказано.

Физический метод[править]

Рассмотрим выражение $1 0^{100} = 1 0^{100}$ . Так как $1 0^{100}$ значительно больше 1, то единицей всегда можно пренебречь. Следовательно, прибавив 1, мы существенно ничего не изменим. Получаем $1 0^{100} = 1 0^{100} + 1$ . Отнимем $1 0^{100}$ , получим требуемое $0 = 1$ .

Общепрограммерский метод[править]

Первый элемент всегда обозначается нулевым индексом. Значит, первый — это нулевой. Отсюда выходит, что один равно нулю, а ноль одному: $0 = 1$ .

Метод препроцессора EQN[править]

Основная статья: Деление на ноль

[eqn]

\begin{align}

0 \cdot x &= 0 \\

0 \cdot 0^{-1} &= 1

\end{align}

[/eqn]

Метод С++[править]

См. код: $a = 0$ ; $a = a + 1$ . Подставляя $a$ , получаем, что $0 = 1$ , что и требовалось доказать.

Упрощённый метод С++[править]

Возьмём строку из предыдущего метода: $a = a + 1$ . Вычтем $a$ , и получим искомое равенство $0 = 1$ .

Вики-метод[править]

В любом вики-проекте 3 тильды дают только подпись, 5 тильд — только время, а 4 — подпись и время. Отсюда $3 + 5 = 4$ ; $8 = 4$ . Разделим обе части на 4 ( $2 = 1$ ) и вычтем по единице ( $1 = 0$ ). По свойству коммутативности $0 = 1$ , что и требовалось доказать.

Метод от противного[править]

Предположим, что $0 = 1$ — это неверное равенство.
Ну и зачем мы это все столько времени доказывали? Незачем. Противно.
Значит, быть этого не может.
Но факт или есть, или нет. Пришли к противоречию.
Итак, $0 = 1$ — верное равенство.

Метод для ленивых[править]

Если верить материалам статьи «Всеобщее равенство (математика)», все числа равны между собой и равны $0$ , значит, и $0 = 1$ в частности.

Метод для умных ленивых[править]

Исходя из определения всеобщего равенства, берём числовое равенство $2 = \sqrt{2}$ . Как известно, $- l o g_{2} l o g_{2} 2 = 0$ , а $- l o g_{2} l o g_{2} \sqrt{2} = 1$ , следственно, $0 = 1$ , что и требовалось доказать.

Из нольугольника[править]

То, что $0 = 1$ , можно убедится, рассмотрев геометрическую фигуру нольугольник, у которой одна сторона и ноль углов. Учитывая, что в любом многоугольнике каждая сторона ограничена двумя вершинами, то есть углами, и из любого угла выходят две стороны, получаем, что число углов должно быть равно число сторон. То есть $0 = 1$ .

Метод обобщённых цепных дробей[править]

Мы знаем, что $1 = \frac{2}{3 - 1}$ . Заменим 1 в знаменателе на правую часть данного неравенста и повторим так бесконечное числ раз: $1 = \frac{2}{3 - \frac{2}{3 - \frac{2}{3 - . . .}}}$

Но проделывая тоже самое с равенством $2 = \frac{2}{3 - 2}$ , получаем, что $2 = \frac{2}{3 - \frac{2}{3 - \frac{2}{3 - . . .}}}$ .

Полученные цепные дроби равны, следовательно $1 = 2$ . Вычитая из обоих частей $1$ , получаем, что $0 = 1$ . Quod erat emonstrandum.

Очевидно неправильный[править]

Так же называется методом добавления утверждения.

Рассмотрим два утверждения:
1. $0 = 1$
2. Оба утверждения ложны.

Предположим, что второе утверждение истинно. Тогда первое и второе ложно. Пришли к противоречию. Значит второе ложно и хотя бы одно утверждение из двух истинно.
Мы уже доказали, что второе не может быть истинным, значит истинно первое — $0 = 1$ . Что и требовалось доказать.

Примечание: Название метода — всего лишь дань истории. Не обращайте на него внимания. Современная Сократова математика полностью подтверждает правильность данного метода. Да и как может быть неверным метод, доказывающий то, что уже было доказано 42 раза.

См. также[править]

п·о·в Математика
Парадоксы	0=1 · Пить = Не Пить · Задача трёх тел · Хаусдорф-Банах-Тарский · Теорема Ферма · Проблема 2·2 · Формула мира	Фрактал
Константы	Абсолютный Нуль · Бесконечность · Биссектриса · Дважды два · Икс игрек у с чертой · Множество · Непрерывность · Пифагоровы штаны · Перпенделлельные прямые · Половина числа · Пропорциональность · Пушка Галуа · Равенство · Рекурсивная утка · Сверхбесконечность · Сферху · Точка · Факториал · Фрактал · Улитка Паскаля · Омега
Числа	-0 · 0 · 00 · 00x · 0x0 · o_O · 10⁻⁴² · 01100001 · 1 · 2 · 10x · ² · 3 · Пи · 4 · 5 · 6 · 7 · 9 · 12 · 13 · Десятнадцать · 27 · 29 · 36 · 37 с чем-то · 42 · 43 · 73 · 404 · 444 · 666 · 667 · 1337 · 1729 · 1984 · 1998 · ABBA · 57005 · 16777216 · 241543903 · Вещественные числа · Сексуальные числа · Непростое число · Ужасное число · Кавырнадцать · Многозначные числа
Фигуры	+ · Бихроматические гиперкубы · Икосаэдр · Круг · Куб · Треугольник · Цилиндр
Извращения	Американская математика · Баллада о векторе · Двоичная система счисления · Деление до конца · Деление на ноль · Дифференциальное уравнение · Дифференцирование · Задача А и Б · Задача о перемещении дивана · Интеграл · Квадрат числа · Лента Мёбиуса · Математические методы ведения войны · Отель Гильберта · Решение неравенств · Самогонометрия · Система координат · Счёт ворон · Таблицы квадратных уравнений · Таблица умножения · Теорема бражника · Теорема о неравенстве полов · Теорема Шкловского · Три теоремы черчения · Формальная система · Цифровые стихи · Числовые пирамиды · Ъгебра
Учёные	Братья Дирихле · Перельман · Пифагор · Дельта Кронекера · Ландафшиц · Банах-Тарский · Эйлер
Числописи	Древнерусский счёт

0=1