Пифагор
Штанина — половина брюк.~ Пифагор
Пифагор — модный древнегреческий портной VI века до н. э. Специализировался на мужской одежде.
Друг и товарищ Пифагора древнегреческий поэт Эсхил придумал для первого его ателье рекламный слоган «Пифагоровы штаны на все стороны равны!»
Первое ателье Пифагора («древнее») находилось на о. Самос. Спасаясь от налогового гнета древнегреческого тирана Поликрата, Пифагор эмигрировал в древнюю Италию. Там в древнем городе Кротоне он открыл второе свое ателье («новое»), но теперь предпочел особо не афишироваться.
В процессе работы постоянно искал способы оптимального раскроя материалов. Преуспел, что доказывается тем фактом, что имя Пифагора дошло до наших дней, а имена всех остальных портных древней Греции забыты, видимо, их поглотил Левиафан. Пифагоровские методы оптимизации налогов кройки и шитья были переоткрыты в 1939 году Канторовичем Л. В.
Скромность ремесла, которым занимался Пифагор, объясняет тот факт, что до наших дней не дошли практически никакие другие достоверные сведения о нем. Разнообразные философские и религиозные учения и Всё такое, что традиционно связывается с именем Пифагора, на самом деле принадлежало его многочисленным древнегреческим заказчикам (пифагорейцам), которые любили толпиться в его ателье в ожидании примерок.
Теорема Пифагора[править]
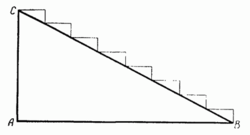
Для качественных выкроек прямых треугольных вырезов Пифагор придумал собственный метод, который почтительно прозвали теоремой.
Пифагор первым из портных задался вопросом как соотносится длина гипотенузы с длиной катетов прямого треугольного выреза. «А что если представить гипотенузу в виде множества микроскопических ступенек, где каждая ступенька одной гранью будет параллельна одному катету, а второй гранью — параллельна другому? Тогда спроецировав параллельные грани ступенек на соответствующие катеты выреза получим наглядное отображение длины его гипотенузы относительно его катетов.» — подумал Пифагор.
В пределе ступеньки сливаются с гипотенузой, а потому длина их граней в пределе будет равна длине гипотенузы. Не сложно наглядно убедиться, что при любом уменьшении ломаной линии из ступенек длина суммы граней еë ступенек идеально равна длине суммы обеих катетов треугольника. То есть . Что и требовалось доказать.

