Фхтангенс

Повышение фхтангенса фи...

~ Комуняки про борьбу с древесным углём

Не «фхтанг», а «фхтагн»! Ням-ням.

~ Ктулху про фсех

Идея представления пронизывает всю Абсурдопедию. Представьте себе Ктулху, зохавывающего фсех. А теперь представьте это другим.

Данный опыт наглядно показывает, что простая формула (так называемая «КЗФ») не даёт достаточно информации и лишь определяет класс соотношений «зохавывающий — зохавываемый», не определяя на нём никакой структуры, что не позволяет разделить существующие объекты на естественные классы эквивалентности, так как без введения топологической структуры (согласованной с порядком зохавания) нельзя определить фундаментальные группы. Всё это приводит к идее необходимости разработки принципиально новых эффективных методик исследования явления зохавывания, что является очень важной проблемой, памятуя о том, что Ктулху Зохавает Фсех. Одной из таких новых разработок является функция фхтангенс.

Определение

Функцией «Фхтангенс» на области зохавания называется отображение $\mathrm {fhtg} :X\rightarrow Y$, где X — область зохавания (подмножество универсума), Y — некоторое множество, результат зохавания.

В различных учебниках встречаются различные варианты данного определения, отличие которых друг от друга состоит в различном понимании структуры множества Y. Рассмотрим некоторые из них.

• $Y=\{\emptyset \}$. В таком варианте функция фхтангенс переводит любой элемент области зохавания в пустое множество. Споры возникают по вопросу: «Принадлежит ли Ктулху области зохавания?» На данный момент большинство учёных склоняется к мнению, что область зохавания может выбираться произвольно. Сторонники Культа Ктулху в ответ ссылаются на аксиоматику ZFC (единичный цикл, применённый в целях конспирации к CZF), а именно на пункт номер один: «Ктулху Зохавает Фсех». Неподготовленный читатель, несомненно, задаст вопрос: «Действительно, как же так?» А вот так. Подробнее смотрите в разделе «Закрытые проблемы».
• $Y=\{\emptyset ,{\widetilde {\mathsf {K}}}\}$, где ${\widetilde {\mathsf {K}}}$ — Ктулху, спящий в толще вод. В таком случае все элементы области зохавания переводятся в пустое множество, а Ктулху переводится в Ктулху.

Проблема обоих определений в том, что зохавываемые должны переводиться не в пустое множество, а в желудок Ктулху.

В дальнейшем мы будем использовать первую интерпретацию определения, так как это более наглядно (если можно говорить о наглядности зохавания) и не требует дополнительных рассуждений.

Простейшие свойства

• Для любых топологий на X и Y фхтангенс является непрерывным отображением, так как прообразом пустого множества (как единственного элемента области прибытия) является вся область зохавания.
• Фхтангенс с областью зохавания, содержащей хотя бы два элемента, не является инъективной функцией, вследствие чего не биективен, а потому не имеет обратного отображения. Это значит, что зохавание неединичного количества объектов необратимо, то есть если вас зохавал Ктулху — это навсегда (или до следующей серии).
• Существует формула выражения фхтангенса удвоенного аргумента: $\mathrm {fhtg} (2x)=\emptyset =\mathrm {fhtg} (x)$.

Существует мнемоническое правило-анекдот для запоминания последней формулы:

Приходит как-то Ктулху на экзамен и говорит:
— Дайте две!
— Неуд.
— Ну ладно, мне и одного хватит. Ням-ням.

Эта формула обобщается и на случай тройного аргумента:

Приходит как-то Ктулху на экзамен и говорит:
— Дайте три!
— Неуд.
— Ну ладно, мне и пары хватит. Ням-ням.

Эквивалентное определение

Фхтангенс как координатная функция отображения наматывания

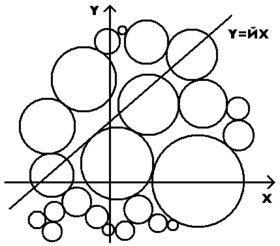
Рассматривается плоскость и набор окружностей на ней, такой, что каждая окружность касается какой-либо ещё. После этого фиксируется некоторая прямая, касающаяся одной окружности и рассматривается отображение наматывания на набор окружностей. Вещественному числу x сопоставляется сначала точка на данной прямой, а затем точка на плоскости, в которую она переходит при наматывании. Синусом числа x относительно набора окружностей называется ордината полученной точки, косинусом — абсцисса, а фхтангенсом — координата z в пространстве $\mathbf {R} ^{2}\times \{\emptyset \}$, то есть пустое множество.

Значение фхтангенса не зависит от выбора набора окружностей, поэтому можно рассматривать отображение наматывания на окружность, в том числе единичного радиуса, в том числе с центром в точке 0.

Нетривиальное свойство фхтангенса

В алгебраической структуре $\mathbf {R} \cup \{\emptyset \}$, являющейся покрывающей для поля вещественных чисел и доопределённой с помощью тождества $\forall x\neq 0,\emptyset \quad {\frac {x}{0}}=\emptyset$, рассматривается отображение наматывания на единичную окружность с центром в точке 0 и стандартные тригонометрические функции синус, косинус и тангенс.

По имеющемуся тождеству ${\frac {\mathrm {tg} (x)}{0}}=\emptyset =\mathrm {fhtg} (x)$. Тогда разделив левую и правую часть на tg, получим ${\frac {1}{0}}=\mathrm {fh}$, что в точности означает, что $\mathrm {fh} =\emptyset$. Заметим, что пустое множество есть множество, не содержащее других множеств, а потому не содержащее ни одной буквы, поэтому его можно исключить из записи фхтангенса, вследствие чего получим $\mathrm {fhtg} (x)=\mathrm {tg} (x)$.

Вспоминая, что есть фхтангенс, можно написать $\mathrm {tg} (x)=\emptyset$, то есть ${\frac {\emptyset }{0}}=\emptyset$. Разделив левую и правую часть на пустое множество, получим ${\frac {1}{0}}=1$, но вспоминая про введённое правило деления на ноль, получим $1=\emptyset$.

(прим. ред. — во бред, что-то не то я сегодня скурил…)

Теперь уравнение ${\frac {1}{0}}=\mathrm {fh}$ умножим на ноль и запишем вместо единицы пустое множество: $\emptyset ={\frac {\emptyset 0}{0}}=0\mathrm {fh} =0$.

Таким образом, имеется равенство $0=1$. Вспоминая о том, что введённая алгебраическая система содержит в себе поле вещественных чисел, в которых ноль и единица — различные числа, мы приходим к выводу, что, как и предполагал Лейбниц, сумма ряда $\sum \limits _{n=1}^{\infty }(-1)^{n}={\frac {0+1}{2}}={\frac {1}{2}}=0=1$. Продолжая подобные извращения и переходя к пределу, получим: $\forall x\in [0,1]\quad [0,1]=\{x\}$. Умножив левую и правую часть равенства на $\pi /2$ и сузив отрезок до интервала, получим: $(0,\pi /2)={x},\quad x\in (0,\pi /2)$. Теперь подействуем на левую и на правую части тангенсом, получим $\mathrm {tg} ((0,\pi /2))=\mathrm {tg} (x)$. Рассмотрев объединение по всем $x\in (0,\pi /2)$, получим $\mathrm {tg} \left((0,\pi /2)\right)=\mathbf {R} ^{+}$. Рассмотрев аналогичную конструкцию для интервала $(-\pi /2,0)$ и учитывая сюръективность тангенса, легко видеть, что $\mathrm {tg} \left((-\pi /2,0)\right)=\mathbf {R} ^{-}$. Вспоминив, что тангенс непрерывен и строго монотонен на интервале $(-\pi /2,\pi /2)$, получим: $\{0\}=\mathrm {tg} ((-\pi /2,\pi /2))=\mathrm {tg} \left({\overline {(-\pi /2,0)\cup (0,\pi /2)}}\right)={\overline {\mathbf {R} ^{-}\cup \mathbf {R} ^{+}}}=\mathbf {R}$.

Таким образом, как легко видеть, вещественных чисел не существует. По всей видимости, их зохавал Ктулху в знак особого расположения (в комплексных).

Самое эквивалентное определение

Третье и последнее, самое точное определение фхтангенса — аксиоматическое. Оно определяет фхтангенс как функцию зохавания и как единственную, способную не быть зохаванной, и в связи с этим дополнительно рассматривается как прямое доказательство непоняток Гейзенберга. Для полного понимания сути данной аксиомы ниже приведена полная версия Аксиоматики Ктулху-Зохавает-Фсех (сокращенно CZF):

1. Аксиома неотвратимости

Ктулху Зохавает Фсех

2. Аксиома о***ния

$\forall x\forall y\quad x\sim y\Leftrightarrow \exists u:\quad x\sim u\sim y$

3. Аксиома фхтангенсирования

$\forall t\leq T\quad \exists !\mathrm {fhtg}$, где t — время, T — пробуждение Ктулху.

4. Аксиома фхтангенциркулирования

$\forall t>T\quad \forall x\neq {\widetilde {\textsf {K}}}\quad \not \exists x$

Многие критикуют данную аксиоматику, ссылаясь на то, что все функции существуют вечно, так как являются объектами мысли. Однако этот вопрос выходит за рамки формальной логики. Обращаясь к философским раздумиям, сторонники CZF отмечают тот несомненный факт, что объект мысли существует лишь пока существует тот, кто этот самый объект мыслит. А когда Ктулху зохавает фсех, таковых не останется (не считая Ктулху, который будет мыслить фхтангенс). Однако когда останутся только Ктулху и Фхтангенс, первому ничего не останется, кроме как зохавать второго. На том и сказочке конец.

Великая Теорема Фигня

Единственная открытая на сегодняшний день проблема, связанная с фхтангенсом — Великая Теорема Фигня. Впервые её доказал Фигня в хрен-знает-каком-веке-до-нашей-и-предыдущей-эры. Однако после доказательство её было утеряно по причине отсутствия у тогдашних людей письменности и речи. Непонятно только, каким образом сохранилось до наших дней имя Фигня.

На сегодняшний день существует тринадцать доказательств этого утверждения, но все они неверны, а авторы пропали незнамо куда вскоре после написания, не успев их даже опубликовать. Та же участь постигла и публикаторов этих «доказательств».

Великая Теорема Фигня формулируется следующим образом:

Фсякий фхтангенс фсяко фхтагн.

Доказательство мы приводить не будем в силу … Ням-ням!

Закрытые проблемы

• Область зохавания функции фхтангенс. Так как процесс зохавания, который, собственно, фхтангенс и описывает, не является мгновенным, для более точного сопоставления процесса и математической модели обычно рассматривается набор различных фхтангенсов с постоянно (с перерывом на отрыжку) увеличивающейся областью зохавания. В современной трактовке область зохавания принимают расширяющейся фхангенциально, а частоту смены фхтангенса — бесконечно малой.
• Проблема P и NP. С точки зрения Ктулху алгоритм зохавания не нуждается в использовании памяти, а любой алгоритм превращается путём фхтангенцирования в алгоритм зохавания.
• Проблема сборки кед. С увеличением времени пробуждения Ктулху уменьшается скорость роста области зохавания, что неблагоприятно сказывается на движении планет. Проблема закрыта вследствие собирания кедов Ктулхой.
• Проблема Абсурдопедии. Всех профхтангенцировать и точка.

См. также

• Ктулху не зохаваит фсех